循环神经网络

基础

sequence

时序模型：当前数据和之前观测的数据相关

  • 统计工具：在时间t，观察到的价格Xt
  • 概率计算 序列模型
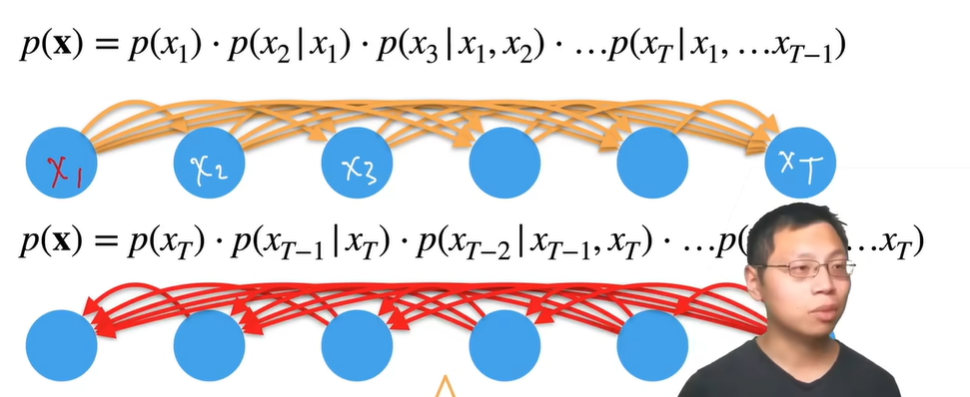
  • 自回归模型 给定前面t-1个数据来预测第t个数据
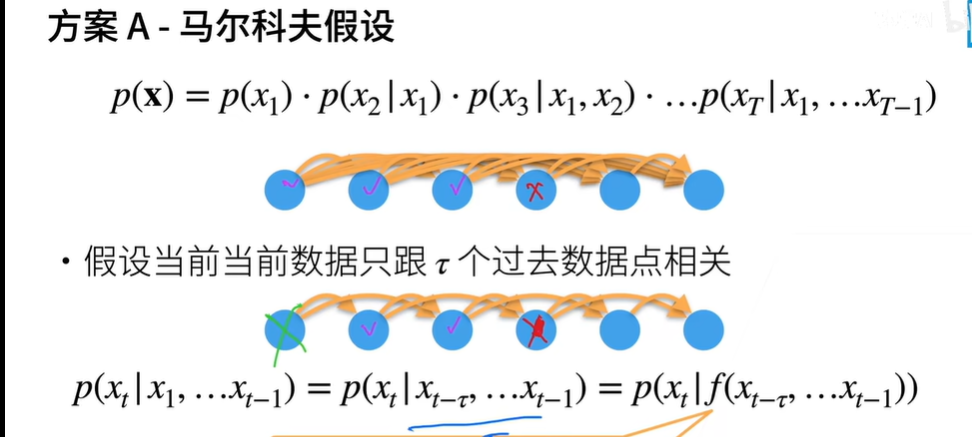
  • 马尔可夫模型 假设当前之和最近少数数据相关
    • 使用xt−1,…,xt−τ 而不是xt−1,…,x1来估计xt
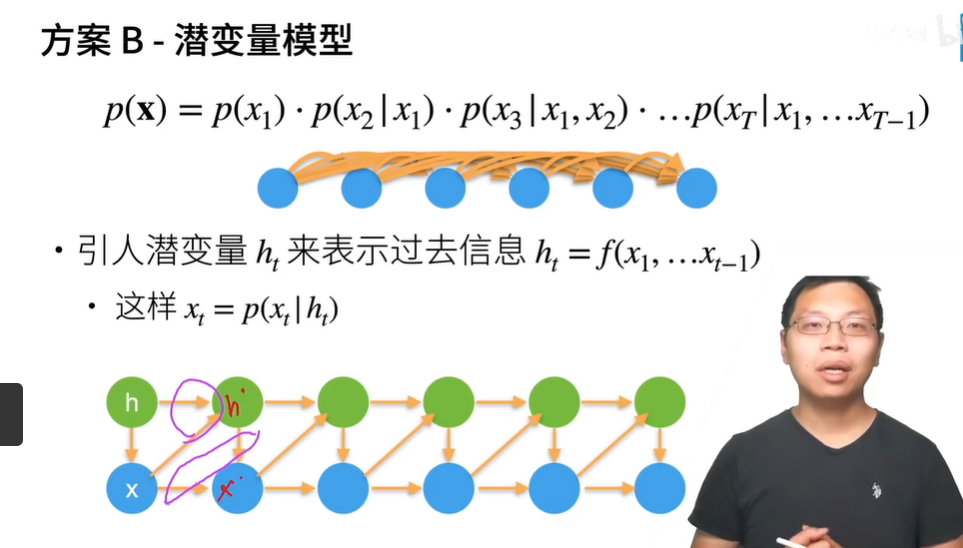
  • 潜变量模型 使用潜变量概况历史信息
    • 保留一些对过去观测的总结ht， 并且同时更新预测x^t和总结ht。 这就产生了基于x^t=P(xt∣ht)估计xt， 以及公式ht=g(ht−1,xt−1)更新的模型。 由于ht从未被观测到，这类模型也被称为 隐变量自回归模型（latent autoregressive models）。
  • k步预测：我们必须使用我们自己的预测（而不是原始数据）来进行多步预测：对于直到xt的观测序列，其在时间步t+k处的预测输出x^t+k 称为k_步预测_（k-step-ahead-prediction）。 由于我们的观察已经到了x604，它的k步预测是x^604+k。
  • 这么单纯的k步预测结果超级差，原因是：
    • 错误的累积： 假设在步骤1之后，我们积累了一些错误ϵ1=ϵ¯。 于是，步骤2的输入被扰动了ϵ1， 结果积累的误差是依照次序的ϵ2=ϵ¯+cϵ1， 其中c为某个常数，后面的预测误差依此类推。 因此误差可能会相当快地偏离真实的观测结果。 例如，未来24小时的天气预报往往相当准确， 但超过这一点，精度就会迅速下降。

代码实现

对于feature的处理
此时为net的输出单个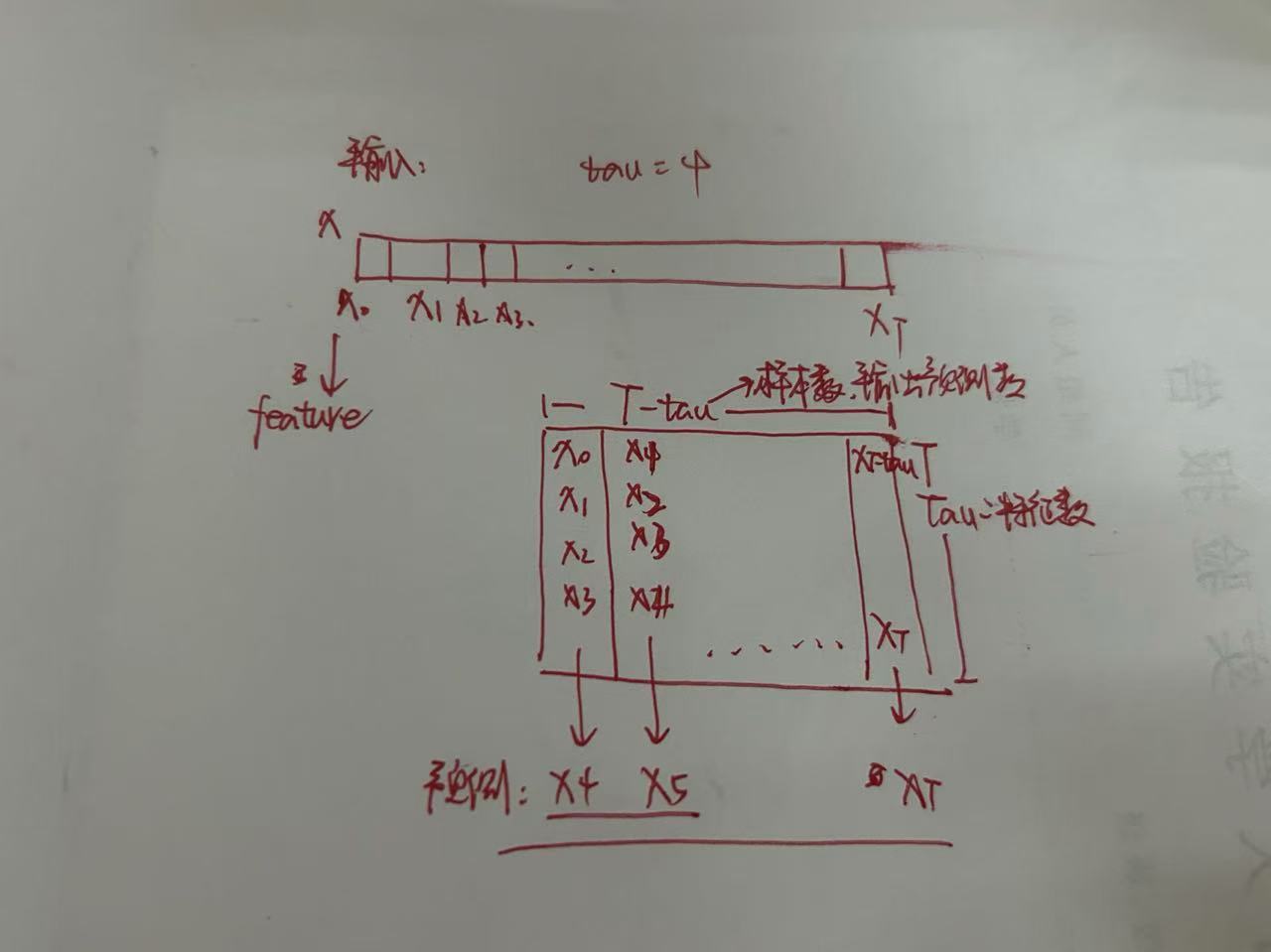

k步预测的单个输出和批量输出（向量）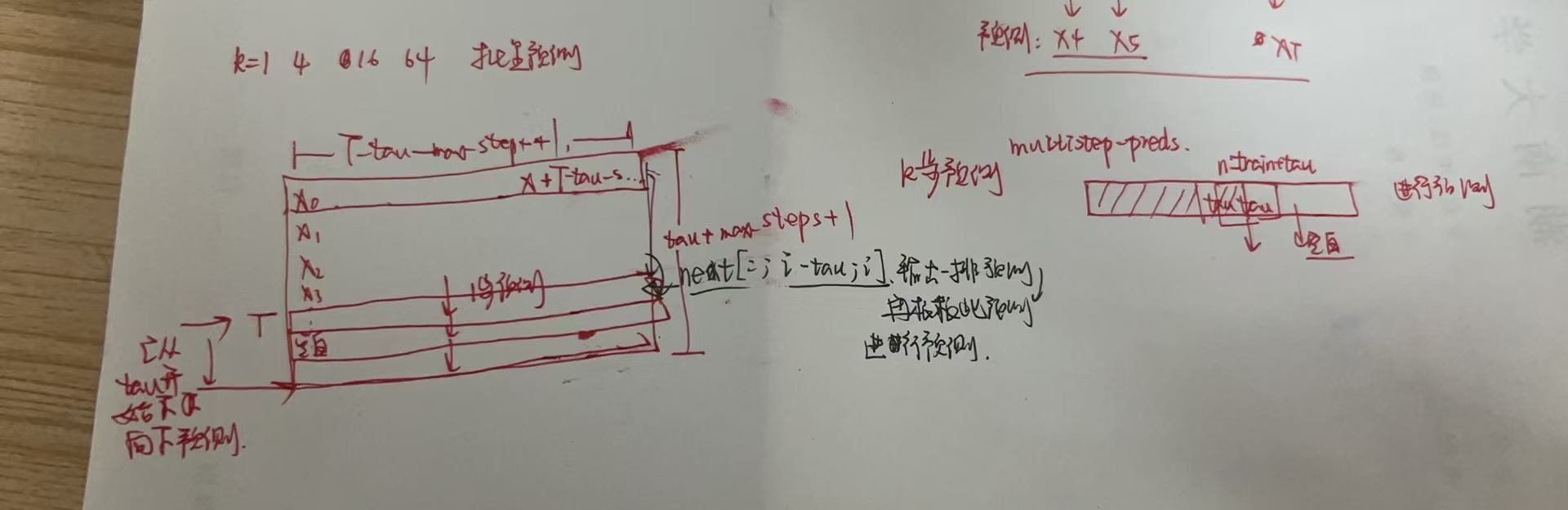

文本预处理

  • re库 正则表达式操作…
  • 读取文档time_machine 处理文档，忽略大小写和标点符号
    • [ re.sub(‘[^ A-Za-z]+’, ‘ ‘, line).strip().lower() for line in lines ]
  • 词元化 tokenize
    • token是文本的基本单位，返回由token组成的列表
    • 这里就暴力的将其拆分为单词 或者字符
    • list 将一些可迭代对象转化为列表类型
  • 构建词表 将模型输入的词源映射到从0开始的数字索引
    • 语料：对训练集的词元进行统计，得到的统计结果为语料
    • 根据每个唯一词元的出现频率，为其分配一个数字索引。 很少出现的词元通常被移除，这可以降低复杂性。
    • 另外，语料库中不存在或已删除的任何词元都将映射到一个特定的未知词元< unk >

语言模型

估计文本序列的联合概率

  • 利用计数建模
    • 条件概率P(deep,learning,is,fun)=P(deep)P(learning∣deep)P(is∣deep,learning)P(fun∣deep,learning,is).
    • n(x)和n(x,x′)分别是单个单词和连续单词对的出现次数
  • 马尔科夫模型和n元语法
    • n元语法 tau = n 比如二元语法和之前的一个元素相关，三元语法和前两个元素相关
    • 复杂度降低O( tau )

代码实现

  • 可以看到有很多词没啥意义，可以被过滤，比如thre is in that 啥的 被称为stop words
  • n元语法实现
    • 将n个token绑定到一起，计算freq

    • 当序列太长没法被模型一次性处理时，希望能够拆分这样的序列方便模型读取
      但是如果我们固定了如图上三段的拆分，那么段和段之间的那一小块（红色方块）我们就没有办法读到，所有我可以采用策略来避免这种情况
  • 随机采样策略 random sampling
    • 随机地生成一个小批量数据的特征和标签以供读取，在随机采样中，每个样本都是在原始的长序列corpus上任意捕获的子序列
    • corpus原始长序列，batch_size 为小批量中子序列的样本数目(几个子序列），num_steps为子序列中预定义的时间步数（每个子序列多长）
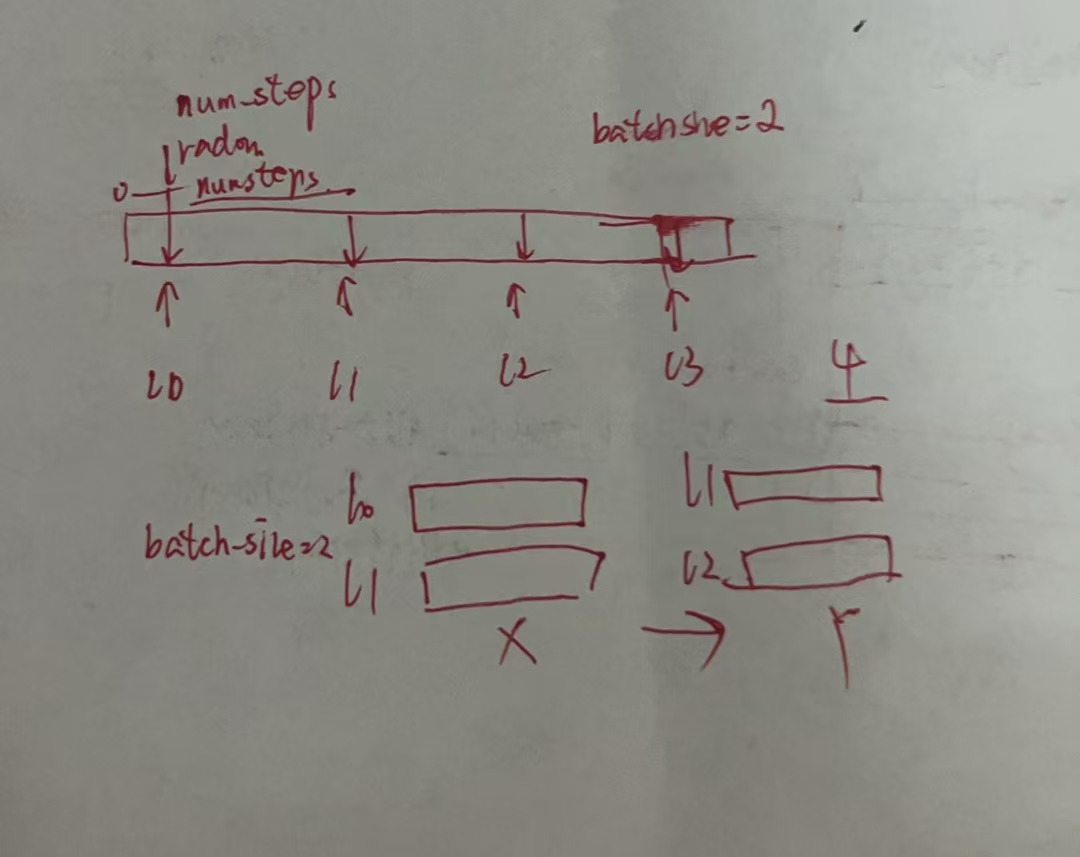
    • 所以也可以把numsteps理解为tau
    • 此时的x,y如图对于x,23，我们要预测出y的24，2324，我们要预测出25，一次类推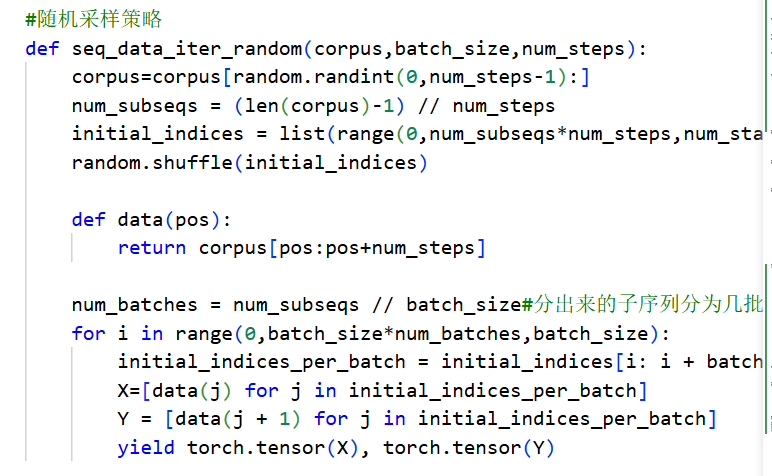
  • 顺序采样策略
    • 保证相邻的小批量之间序列是连续的

RNN

  • 对隐状态使用循环计算的神经网络称为循环神经网络（RNN）。

  • 潜变量自回归模型

    • 使用潜变量ht总结过去信息
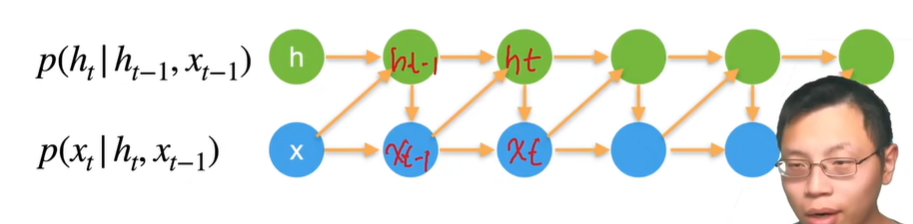
    • 升级变成rnn

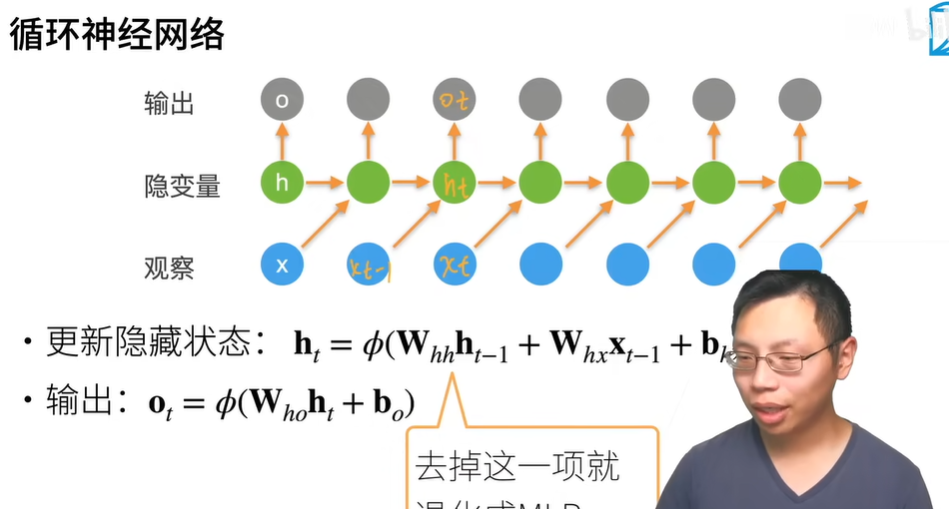
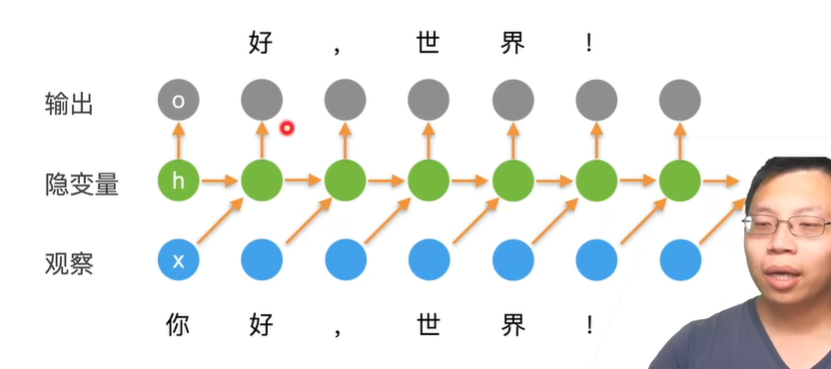
  • 跟多层感知机的区别，Ot的输出是由Xt-1决定的，在mlp里面，输入Xt,输出Ot，不存在这样一个时间的关系

困惑度 perplexity

困惑度为k，k个词都有可能
困惑度的最好的理解是“下一个词元的实际选择数的调和平均数”。

梯度裁剪

从零实现代码

  • 独热编码：将每个索引映射为不同的独热向量
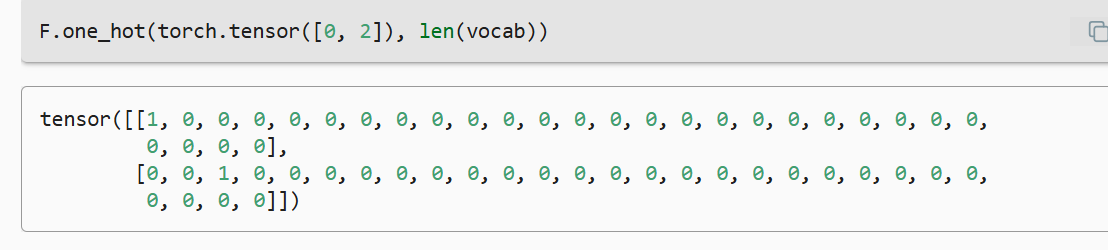
  • 小批量数据形状是（批量大小，时间步数）
  • one_hot函数将这样一个小批量数据转化为三维向量，张量的最后一个维度等于词表大小（len(vocab)）。
  • 我们经常转换输入的维度，以便获得形状为 ==（时间步数，批量大小，词表大小）==的输出。

初始化模型参数

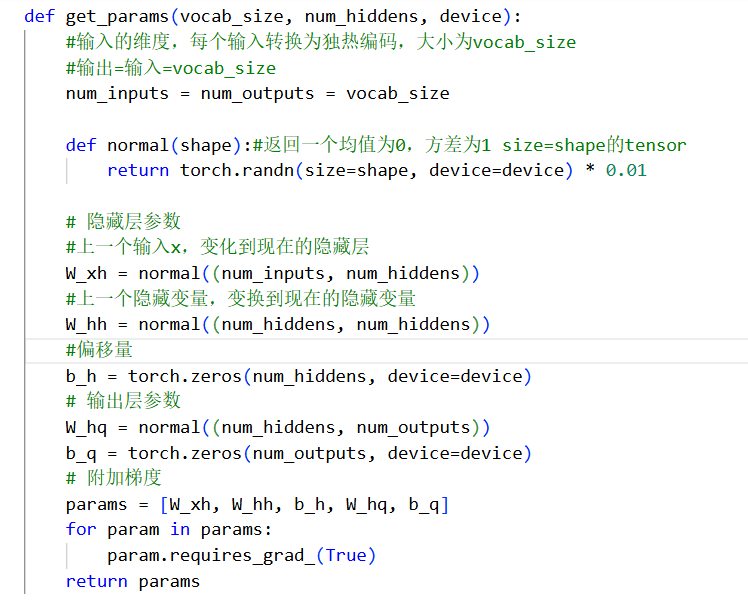
在初始化的时候返回隐状态

在0时刻我们没有隐藏状态，所以要初始化

定义rnn函数

定义一个类包装所有函数


输出形状是（时间步数×批量大小，词表大小）， 而隐状态形状保持不变，即（批量大小，隐藏单元数）。

预测函数

预测给定句子的开头后面可能会输出什么

预热期，不输出，在循环遍历prefix中的开始字符时， 我们不断地将隐状态传递到下一个时间步，但是不生成任何输出。 因为在此期间模型会自我更新（例如，更新隐状态）， 但不会进行预测。
先扔一个开头的字符进行预热，把所有的字符加入output里且更新完隐状态后，再从output末尾进行预测

梯度裁剪

将梯度g投影回给定半径 （例如θ）的球来裁剪梯度g。 如下式：


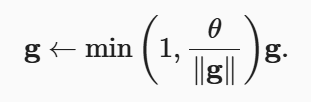
公式看不太懂要死，直接看实现把..

  • 如果没有这一步的话，默认tensor是没有grad的

困惑度

训练

  • 如果我们使用随机抽样，那上一个隐藏状态就跟我们现在的初始隐藏状态没有任何关系，需要重新初始化
  • 如果我们用的顺序采样，那么就可以继续使用上一个隐藏状态，记得把detach_掉

简单实现代码

  • 定义模型
1
2
num_hiddens=256
rnn_layer=nn.RNN(len(vocab),num_hiddens)
  • 初始化隐状态 它的形状是（隐藏层数，批量大小，隐藏单元数）。
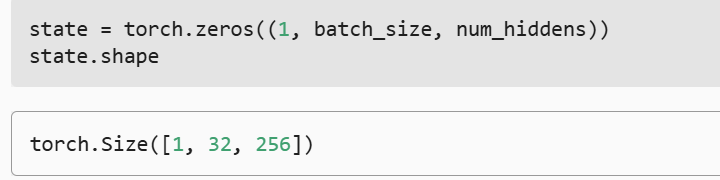
  • 查看一下rnn_layer的输出
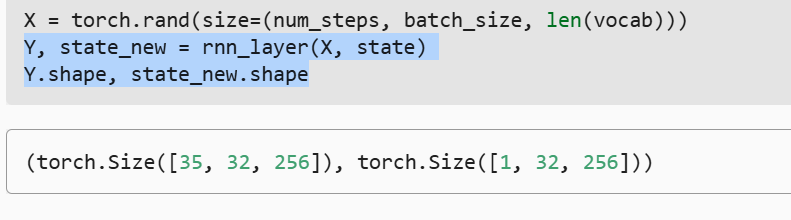
    • rnn_layer=nn.RNN(len(vocab),num_hiddens)
  • 我们要通过rnn_layer和一个线性输出层，构建rnn模型
  • X 输入（num_steps,batch_size,len(vocab)
  • 隐状态 （隐藏层数，batch_size，hiddens）

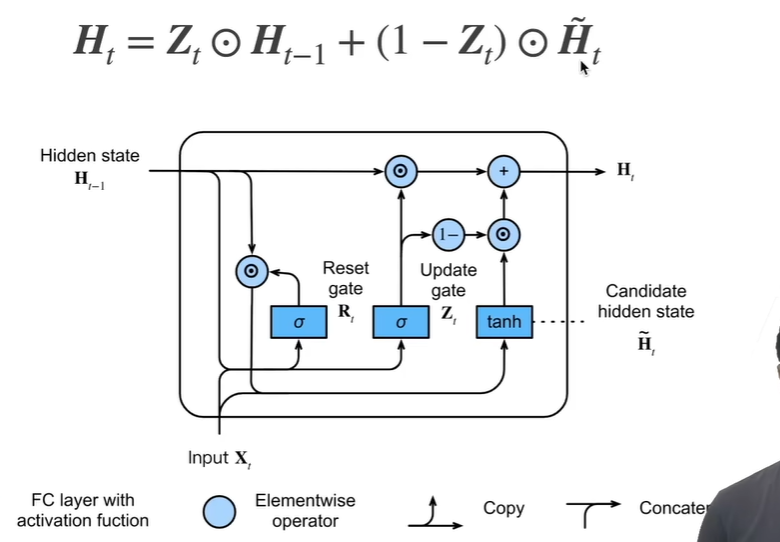
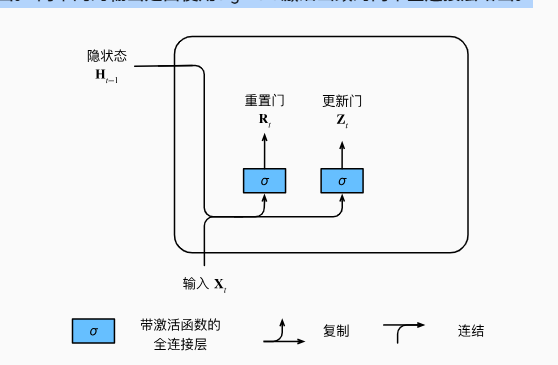
门控循环单元 GRU

  • 重置门和更新门
    • 能关注的机制（更新门）
    • 能遗忘的机制（重置门）
    • 输入是由当前时间步的输入和前一时间步的隐状态给出。 两个门的输出是由使用sigmoid激活函数的两个全连接层给出。
    • 使用sigmoid函数（如 4.1节中介绍的） 将输入值转换到区间(0,1)。

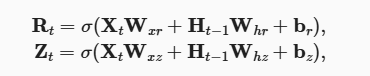
候选隐状态

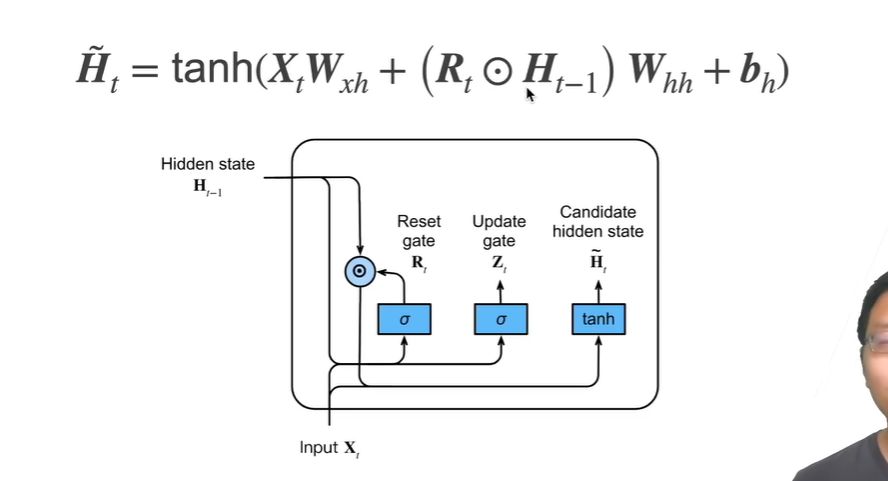
隐状态